mlger

谢希仁计算机网络02-物理层

发表于 2023-10-22 更新于 2023-12-09 分类于计网

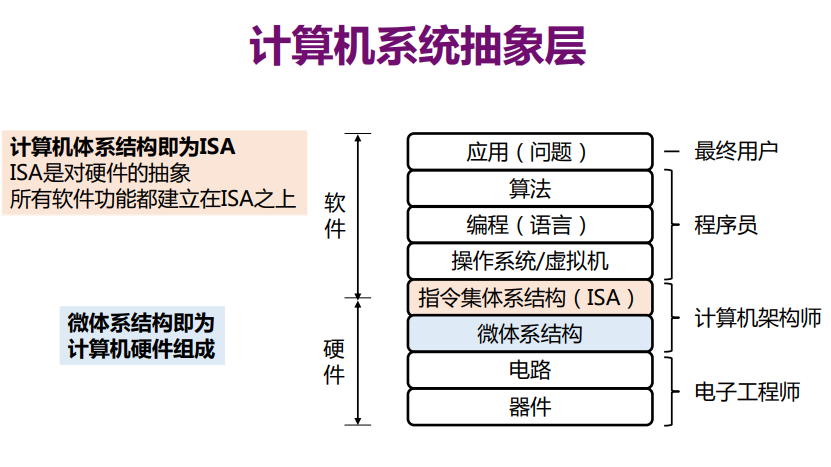
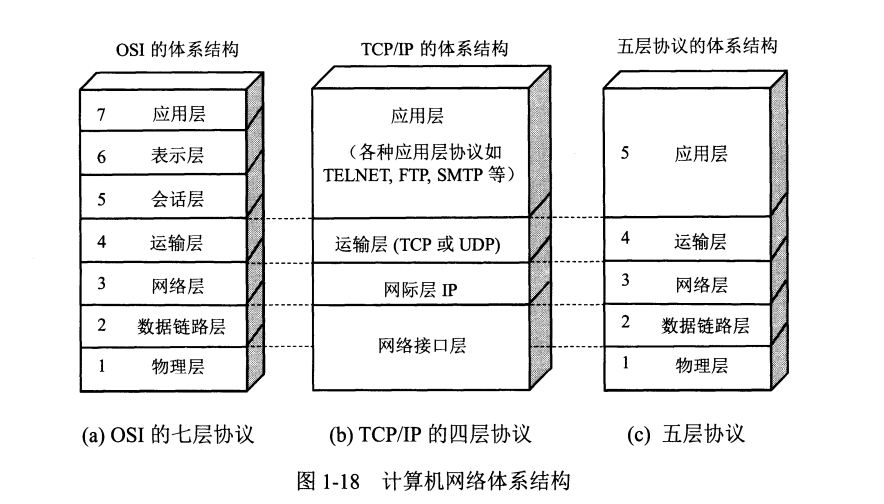
2.1 物理层的基本概念

用于物理层的协议也称为规程(procedure)。

可将物理层的主要任务描述为确定与传输媒体的接口有关的一些特性，即：

(1) 机械特性：指明接口所用接线器的形状尺寸、引脚数目排列等。

(2) 电气特性：指明接口电缆各条线电压范围。

(3) 功能特性：指明某条线某电平的电压的意义。

(4) 过程特性：指明不同功能的各种可能事件的出现顺序。

数据在计算机内部采用并行传输，但在通信线路上一般采用串行传输，因此物理层还要完成传输方式的转换。

2.2 数据通信的基础知识

2.2.1 数据通信系统的模型

数据通信系统可划分为三大部分：源系统（或发送端、发送方）、传输系统（或传输网络）和目的系统（或接收端、接收方）

源系统一般包含两部分：

源点(source)：产生要传输的数据。又称源站或信源。
发送器：将源点产生数据进行编码，之后才能进行传输。如调制器。

目的系统一般包含两部分：

接收器：接受传输信号，并转化为目标设备能处理的信息。如解调器。
终点(destination)：接受比特流

现在很多计算机使用内置的调制解调器，用户在计算机外看不见调制解调器。

通信的目的是传送消息(message)。数据(data)是运送消息的实体。信号(signal)是数据的电气或电磁表现。信号可分为两大类：

(1) 模拟信号，或连续信号：如用户家中的调制解调器到电话端局之间的用户线上的信号。

(2) 数字信号，或离散信号：如用户家中计算机到调制解调器之间，或电话网中继线上传送的信号。使用时间域（或称时域）的波形表示数字信号时，取不同离散数值的基本波形称为码元。

2.2.2 有关信道(channel)的几个基本概念

从通信双方的交互方式来看，有三种基本通信方式：

(1) 单向通信：也称单工通信。如无线电广播，或有线电广播及电视广播。

(2) 双向交替通信：也称半双工通信，双方均可发送，但不可同时发送。

(3) 双向同时通信：也称全双工通信。

单向通信仅需一条信道，而双向交替通信和双向同时通信均需两条。全双工通信效率最高。

来自信源的信号称为基带信号，往往含有较多低频成分甚至直流成分，而许多信道并不能传输这种低频或直流分量，因此必须对基带信号进行调制(coding)。使用载波(carrier)进行调制，把基带信号频率搬移到较高频段，并转化为模拟信号，便可更好在模拟信道中传输。载波调制后信号称带通信号，调制称为载波调制。

2.2.3 信道极限容量

限制码元在信道上传输速率的因素：

(1) 信道可通过频率范围

信道能通过频率范围有限，高频分量往往无法通过信道。高频分量传输时受衰减，接收端受到信号便失去了码元间的清晰界限，此现象称码间串扰。

奈氏准则告诉我们：任何信道中，码元传输速率有上限，超过该上限，则会出现严重码间串扰问题，使接收端对码元的判决称为不可能。

(2) 信噪比

信噪比是信号的平均功率与噪声的平均功率比值，记作 S/N，度量单位为分贝。

香农公式指出，信道的极限传输速率 C 为

$C = W\log_2(1+S/N)\ \ \ (bit/s)$

其中 $W$ 为信道带宽， $S$ 和 $N$ 分别表示信号与噪声的平均功率。

香农公式表面，信噪比越大，极限传输速率越高。对于频带宽度已确定的信道，信噪比也无法继续提高，码元传输速率也达上界，欲提升传输速率，可通过编码的方法让每一个码元携带更多比特信息量。

2.3 物理层下面的传输媒体

传输媒体分为导引型传输媒体和非导引型传输媒体两大类。

2.3.1 导引型传输媒体

1. 双绞线

两根互相绝缘铜导线绞合，以减少对相邻导线的电磁干扰。使用最多地方为电话系统。

模拟运输和数字运输均可使用双绞线，通信距离为几到十几公里。

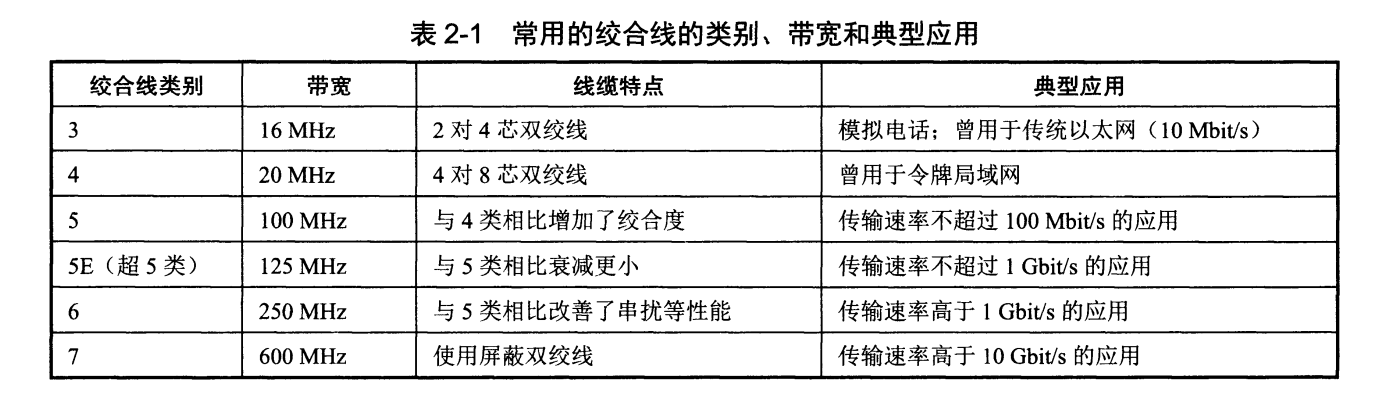
为提升抗电磁干扰能力，可在外面加上一层用金属丝编织成的屏蔽层，称为屏蔽双绞线，简称 STP(Shielded Twisted Pair)。无屏蔽双绞线简称 UTP(Unshielded Twisted Pair) 。

“商用建筑物电信布线标准”—— EIA/TIA-568-A ——规定了 5 个种类的 UTP 标准，最常用的是 5 类线。

2. 同轴电缆

由内导体铜质芯线、绝缘层、网状编织外导体屏蔽层以及保护塑料外层组成。具有良好抗干扰特性，被广泛用于传输较高速率的数据。

目前主要用在有线电视网的居民小区中。

3. 光缆

光纤在发送端有光源，可采用发光二极管或半导体激光器。接收端用光电二极管做成光检测器，可还原出电脉冲。原理是利用光的全反射。

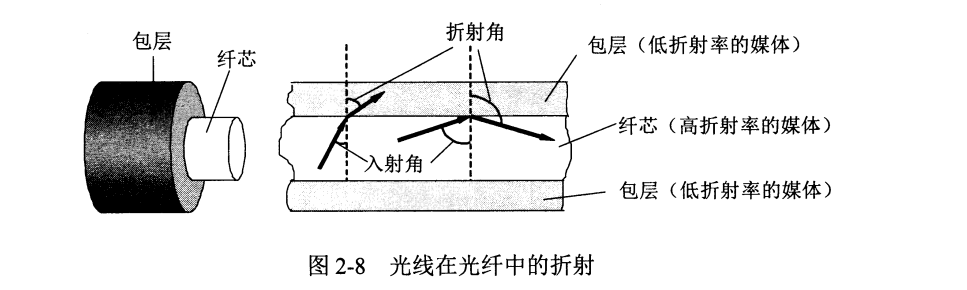
现代工艺可制造出超低损耗光纤，即做到传输数公里而没什么衰耗。这是光纤通信飞速发展的最关键因素。

可以存在多条不同角度入射光线在同一光纤中传输，称为多模光纤。但光脉冲传输时会展宽，因此多模光纤仅适用于近距离传输。

光纤优点：

(1) 通信容量大。

(2) 传输损耗小，中继距离长，对远距离传输经济。

(3) 抗雷和电磁干扰性能好，在大电流脉冲干扰下尤为重要。

(4) 无串音干扰，保密性好。

(5) 体积小，重量轻。

4. 架空明线

在电线杆上架设互相绝缘的明线（铜线或铁线）。许多国家都已经停止铺设，目前我国一些农村与边远地区仍使用。

2.3.2 非导引型传输媒体

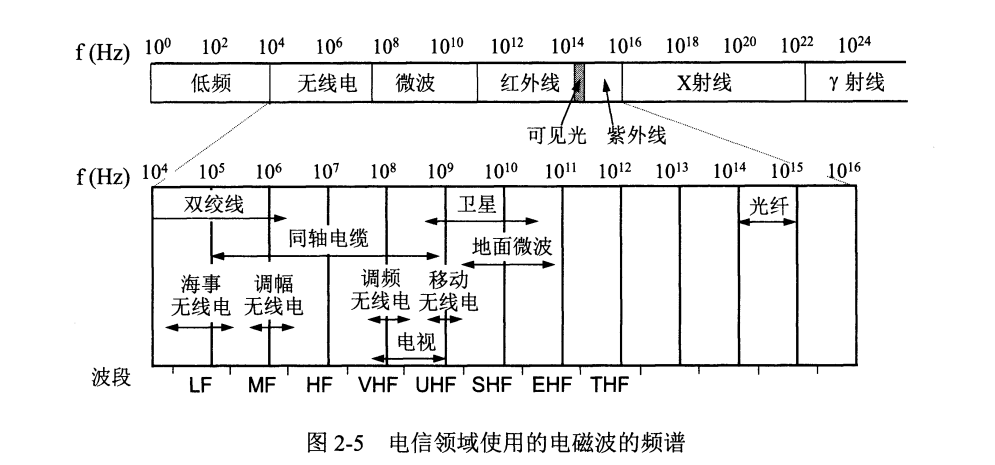
无线传输可使用频段很广，紫外线和更高的波段目前还不能用于通信。

短波通信（即高频通信）主要靠电离层反射，但电离层不稳定产生的衰落现象和反射产生的多径效应，使得短波通信质量较差。因此短波无线电台一般采用低速传输。

2.3.2.1 微波通信

无线电微波通信在数据通信中具有重要地位，频率范围为 $300\ MHz\sim 300\ GHz$ （波长 $1\ m\sim1\ mm$），主要用 $2\sim40\ GHz$ 范围。微波在空间主要是直线传播，会穿过电离层进入宇宙空间，因此不像短波可以反射到地面很远地方。微波通信主要分为地面微波接力通信和卫星通信两种方式。

由于地球是个曲面，微波直线传输距离受到限制，因此需要在两个通讯点间建立若干中继站，进行接力。微波接力通信可传输电话、电报、图像、数据等信息，特点是：

(1) 频率高，频段范围宽，通信信道容量大。

(2) 受到干扰小，质量高。

(3) 建设投资少，见效快，易于跨越山区、江河。

但也有如下缺点：

(1) 相邻站必须直视，不可有障碍物。有时一个天线发出信号也会分成几条略有差别路径，造成失真。

(2) 有时会受到恶劣天气影响。

(3) 隐蔽性和保密性差

(4) 大量中继站使用和维护需要耗费大量人力物力。

2.3.2.2 卫星通信

利用位于约 $3$ 万 $6$ 千公里高空的同步卫星作为中继器。主要优缺点与地面微波通信差不多。但具有较大传播时延。费用较高。

由于在同步卫星轨道架设卫星数量有限，因此在卫星上使用不同频段来进行通信，保证大的通信容量资源。

红外通信、激光通信也用于非导引型媒体。可用于近距离笔记本电脑相互传送数据。

2.4 信道复用技术

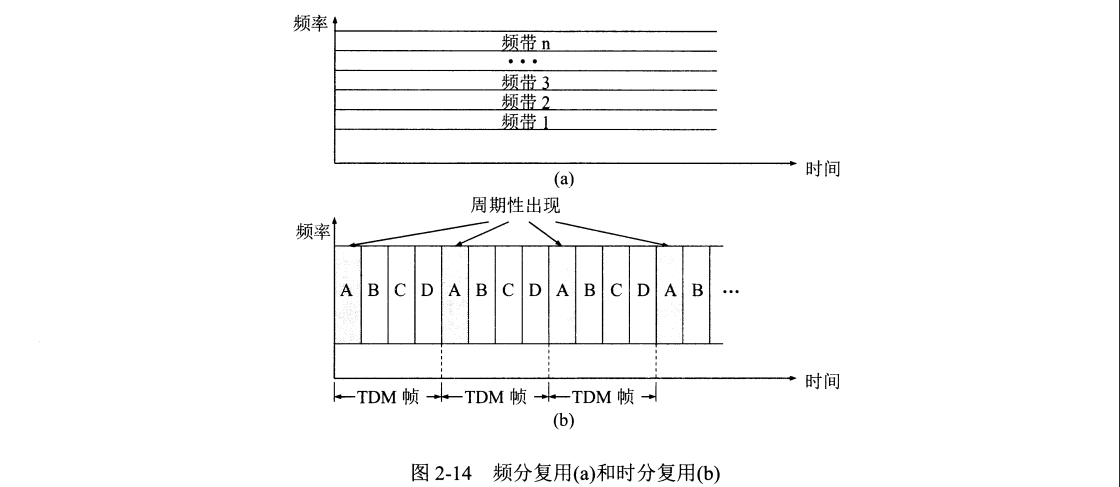
2.4.1 频分复用、时分复用与统计时分复用

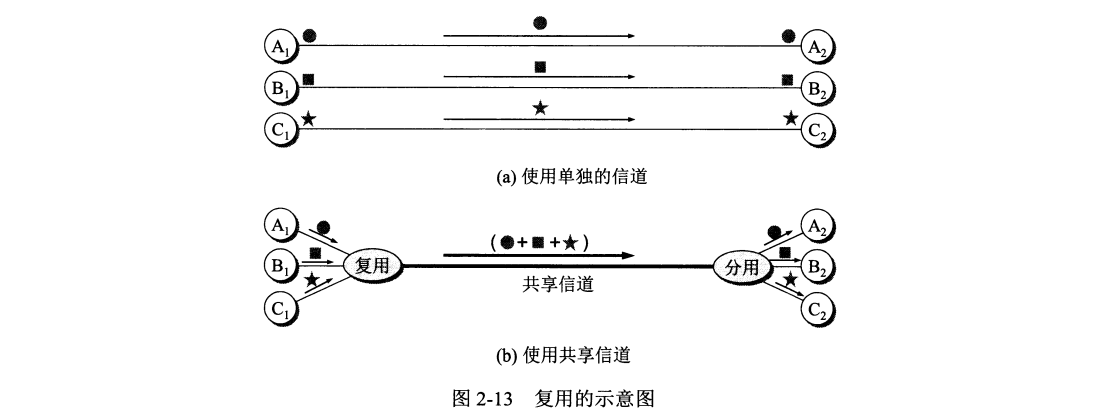
频分复用 FDM (Frequency Division Multiplexing) 的所有用户在同样时间占用不同带宽资源。

时分复用 TDM (Time Division Multiplexing) 则是将时间划分为一段段等长的 TDM 帧，所有用户在不同时间占用同样的频带宽度。

复用器(multiplexer) 和分用器(demultiplexer) 成对使用。

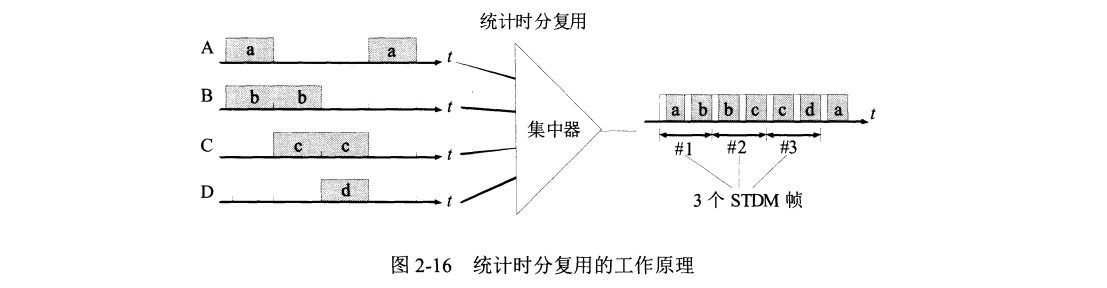
统计时分复用 STDM (Statistic TDM) 是一种改进的时分复用，能明显提高信道利用率。使用集中器(concentrator) 进行复用。集中器也称智能复用器。

2.4.2 波分复用

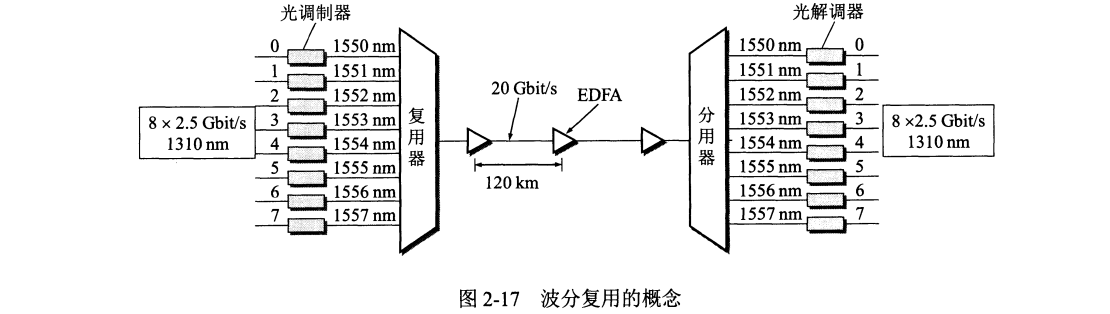
波分复用 WDM (Wavelength Division Multiplexing) 就是光的频分复用。一根光纤复用几十路或更多路光载波信号，使用密集波分复用 DWDM (Dense WDM) 这一名词。

掺铒光纤放大器 EDFA (Erbium Doped Fiber Amplifier) 不需要进行光电转化直接对光信号进行放大。

2.4.3 码分复用

码分复用 CDM (Code Division Multiplexing) 是另一种共享信道方法，也称码分多址 CDMA (Code Division Multiple Access) 。每个用户可以在同一时间用同样频带进行通信。各用户间不会造成干扰，具有很强抗干扰能力，频谱类似于白噪声，不易被敌人发现。

CDMA 中，每一个比特时间再划分为 $m$ 个短的间隔，称为码片 (chip)。通常 $m$ 取 $64$ 或 $128$。一个站如果发送比特 $1$ ，则表示发送该码片，发送 $0$ 则表示该码片的反码。如此每发送 $b$ 个比特，实际信息则扩频为 $mb$ 个比特。该种扩频方式属于直接序列扩频 DDSS (Direct Sequence Spread Spectrum)。另一种扩频方式为 调频扩频 FHSS (Frequency Hopping Spread Spectrum)。

CDMA 要求每一个站分配的码片向量各不相同且相互正交。实际系统采用伪随机码序列。

任何一个码片与自身内积为 $1$，与其反码内积为 $-1$ 。

结合全球定位系统 GPS，所有的站可以同步发送码片序列。若 X 站接受 S 站发送的数据，则需预先知道 S 站特有的码片序列，然后将接受到的信号与 S 站的码片序列作内积，即可解码。

2.5 数字传输系统

早期数字传输系统缺点：

(1) 速率标准不统一。

(2) 不是同步传输。

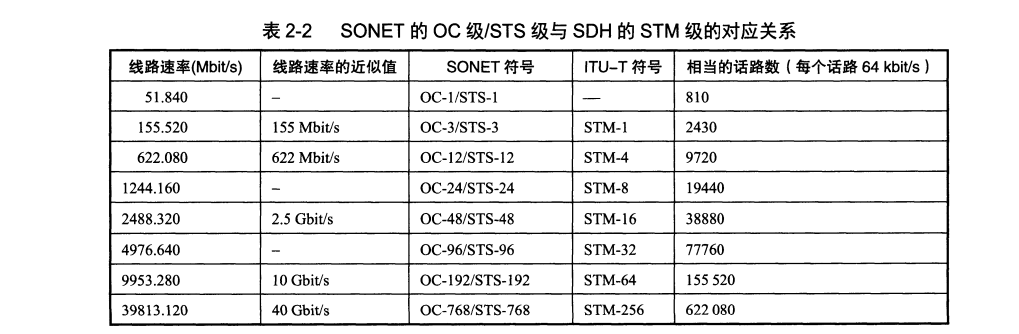
为解决上述问题，美国于 1988 年首先推出一个数字传输标准，叫同步光纤网 SONET (Synchronous Optical Network)。

ITU-T 以 SONET 为基础，制定国际标准同步数字系列 SDH (Synchronous Digital Hierarchy)。 SDH/SONET 标准的制定及各国的统一运用，实现了数字传输体制上的世界性标准。

2.6 宽带接入技术

2.6.1 ADSL 技术

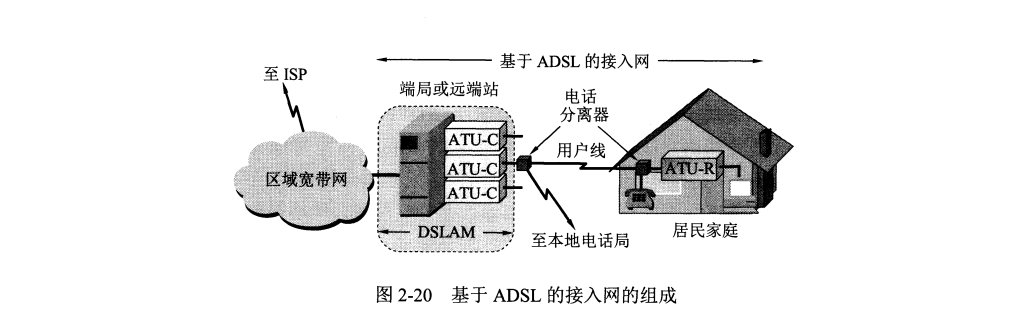
非对称数字用户线 ADSL (Asymmetric Digital Subscriber Line) 技术是用数字技术对现有的模拟电话用户线进行改造，使它能够承载宽带数字业务。下行带宽（从 ISP 到用户）远远大于上行带宽（从用户到 ISP ）。传输距离取决于数据率与线径。

ADSL 在用户线两端各安装一个 ADSL 调制解调器，我国目前采用的实现方法是 离散多音调 DMT (Discrete Multi-Tone) 调制技术。 ADSL 并不能保证固定的数据率。其最大优点是不需要重新布线。

基于 ADSL 的接入网三大组成部分：数字用户线接入复用器 DSLAM (DSL Access Multiplexer)，用户线和用户家中一些设施。 ADSL 调制解调器必须成对使用，把端局和用户家中的 ADSL 调制解调器分别记为 ATU-C（C 代表端局 (Central Office)）和 ATU-R （R代表远端 (Remote)）。用户电话通过分离器 (Splitter) 与 ATU-R 连在一起。

ADSL 技术也在发展，第二代 ADSL 改进的地方主要为：

(1) 通过提高调制效率得到更高的数据率。

(2) 采用无缝速率自适应技术 SRA (Seamless Rate Adaptation)，自适应调整速率。

(3) 改善线路质量测评和故障定位功能。

ADSL 技术并不适用于企业，原因在于企业通常需要使用上行信道发送大量数据给用户。为满足企业需要，ADSL 技术有几种变型，记为 xDSL。

2.6.2 光纤同轴混合网

光纤同轴混合网（HFC 网，HFC 是 Hybrid Fiber Coax 缩写）是基于有线电视网基础上开发的一种居民宽带接入网，主要特点如下：

把原有有线电视网同轴电缆主干部分该换为光纤，从头端连接到光纤节点 (fiber node)。光纤节点光信号转化为电信号，通过同轴电缆传输到每个家庭。

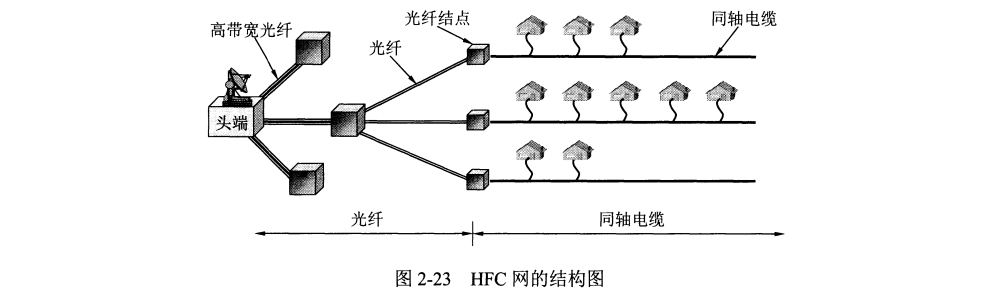
模拟电视机要能够接受数字电视信号，需要一个机顶盒 (set-top box)连接在同轴电缆与电视机之间。若欲接入互联网，还需增加 HFC 网所使用的调制解调器，称为 电缆调制解调器 (cable modem)。

2.6.3 FTTx 技术

光纤到户 FTTH (Fiber To The Home) 两个问题：

(1) 价格高昂。

(2) 一般家庭用户没有这样高的数据率需求。

这种情况下，出现了多种宽带光纤接入方式，称为 FTTx ，x 表示不同的光纤接入地点。

为有效利用光纤资源，光纤干线和用户之间，需要铺设一段中间转换装置即 光配线网 ODN (Optical Distribution Network)，使得数十个家庭用户可以共享一根光纤。五元的逛配线网称为无源光网络 PON (Passive Optical Network)。

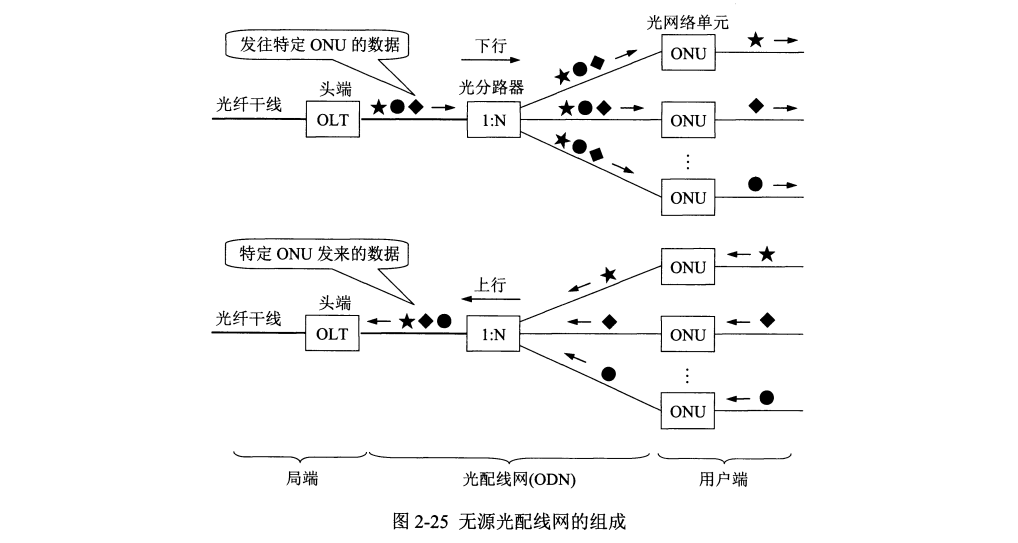
光纤干线与光线路终端 OLT (Optical Line Terminal) 相连，OLT 把收到的下行数据发往无源的 1:N 光分路器 (splitter) ，然后以广播方式向所有用户端的光网络单元 ONU (Optical Network Unit) 发送。

光配线网采用波分复用，上行和下行分别使用不同的波长。

目前已实现了多种不同的 FTTx，如 光纤到路边 FTTC（C 表示 Curb）、光纤到小区 FTTZ（Z 表示 Zone）、光纤到大楼 FTTB（B 表示 Building）、光纤到楼层 FTTF（F 表示 Floor）、光纤到办公室 FTTO （O 表示 Office）、光纤到桌面 FTTD（D 表示 Desk）等等。

计组01-计算机系统概述

发表于 2023-09-08 更新于 2023-12-09 分类于计组

1.1 概念

何为计算机：计算机是指“通用电子计算机”
- 通用：不是专用设备
- 电子：采用电子元器件
- 数字：信息采用数字化形式表示
计算机系统：硬件和软件
何为计算机“组织”：操作单元及其互联连接
- 对编程人员不可见
- 包括：控制信号，存储技术等
何为计算机”结构“：直接影响逻辑程序执行的属性
- 对编程人员可见
- 包括：指令集，表示数据类型的位数等

指令集体系结构： ISA ，有时称为指令系统。 ISA 是一种规约，规定如何使用硬件。
- 可执行指令的集合，包含指令格式、操作种类及操作数的规定
- 指令可以接受的操作数类型
- 操作数所能存放的寄存器组的结构，包括每个寄存器的名称、编号、长度和用途
- 操作数所能存放的存储空间的大小和编址方式
- 操作数在存储空间存放时按照大端还是小端方式存放
- 指令获取操作数的方式，即寻址方式
- 指令执行过程的控制方式，包括程序计数器（PC）、条件码定义等
ISA 与组成之间的关系：计算机组成必须能够实现 ISA 规定的功能，如提供 GPR 、标志、运算电路等，一种 ISA 可以有不同的计算机组成。

1.2 计算机简史

1.2.1 第一代：真空管

ENIAC ：第一台通用计算机，十进制，手动编程
ABC ：第一台电子计算机，不可编程
EDVAC ：冯·诺伊曼架构（普林斯顿架构）
- 三个基本原则：
  - 二进制
  - 存储程序
  - 5个组成部分
    - 主存储器：地址和存储内容
    - 算术逻辑单元 / 处理单元：执行信息处理
    - 程序控制单元 / 控制单元：指挥信息处理
    - 输入设备
    - 输出设备

1.2.2 第二代：晶体管

体积更小、更便宜、发热更少
使用高级语言编程，并为计算机提供了系统软件

1.2.3 第三代：中小规模集成电路

1.2.4 第四代：（超）大规模集成电路

思想：
- 将整个电路安装在很小的硅片上，而不是用分立元件搭成的等价电路
- 晶体管可以通过金属化相互连接，形成电路

1.3 计算机发展

1.3.1 摩尔定律

价格不变时，单芯片上所能包含的晶体管数量每年翻一番 (1965-1969) / 1970年起减慢为每18个月翻一番
影响：
- 更小尺寸带来更多灵活性与可能性
- 成本下降
- 减小电能损耗与冷却要求
- 芯片间连接更少，更可靠

1.4 计算机性能

1.4.1 CPU 性能

计算机设计主要目标：提升 CPU 性能
系统时钟
- 时钟频率： 1s 内执行基本操作的次数
- 始终周期：执行每次最基本操作的时间
指令执行： $CPI_i$ 表示第 $i$ 种指令需要周期数， $I_i$ 表示第 $i$ 类指令条数，则有

$CPI=\frac{\sum_{i=1}^n(CPI_i \times I_i)}{I_c},I_c=\sum_{i=1}^n I_i$

执行一个程序的处理时间表示为

$T=I_c\times CPI \times t$

每秒百万条指令（ MIPS ）：

$MIPS = \frac{I_c}{T\times 10^6}=\frac{f}{CPI\times 10^6}$

每秒百万条浮点操作（ MFLOPS ）：

$MFLOPS=\frac{N_{floating-point\ op}}{T\times 10^6}$

1.4.2 性能设计的基本原则

大概率事件优先原则：对于大概率事件，赋予优先的处理权与资源使用权。

$系统加速比=\frac{总执行时间_{改进前}}{总执行时间_{改进后}}$

Amdahl 定律：
- 部件系统加速比受限于其在系统中所占重要性比例。
- 性能增加的递减规则：改进越，系统获得效果越小

$系统加速比=\frac{总执行时间_{改进前}}{总执行时间_{改进后}}=\frac{1}{(1-局部占比)+ \frac{局部占比}{提升的性能}}$

计算机网络01

发表于 2023-09-05 更新于 2023-12-09 分类于计网

第1章概述

1.1 计算机网络在信息时代的作用

21世纪数字化、网络化、信息化，形成以网络为核心的信息时代。

三大类网络：电信网络、有线电视网络、计算机网络

互联网两个基本特点：连通性和共享

连通性：不论多远，都可便捷地交换各种信息
资源共享：信息共享、软件共享、硬件共享

1.2 互联网概述

计算机网络由若干节点( node )和连接这些节点的链路( link )组成。

节点：计算机、集线器、交换机、路由器等

网络把许多计算机连接在一起，互连网把许多网络通过路由器连在一起。与网络相连接的计算机称为主机。

互联网发展的三个阶段：

由 ARPANET 向互连网发展。 20 世纪 70 年代， APRA 开始研究多种网络互连的技术，称为互联网的雏形。 1983 年 TCP/IP 成为 ARPANET 上的标准协议，互联网诞生。 1990 年 ARPANET 关闭。
- internet （互连网）：指多个网络连接而成的网络
- Internet （互联网）：专有名词
第二阶段特点是建成了三级结构的互联网。分为主干网、地区网和校园网（企业网）。
第三阶段特点是形成了多层次 ISP 结构的互联网。 ISP 译为互联网服务提供商。

计算机网络的分类：

LAN （局域网）
- 特点
  - 作用范围小
  - 多用户访问
  - 高速度
  - 错误率可控
- 设备
  - Hub （集线器）：多端口中继器
  - Bridge （网桥）：
  - Switch （交换机）：
  - Router （路由器）：分组交换，转发收到的分组
WAN （广域网）
- 特点
  - 作用范围大
  - 通过链路传输
  - 速度相对较低
  - 错误率较难控制
- 设备
  - Router （路由器）：
  - Modem CSU/DSU TA/NT1

Boring！

1.3 互联网的组成

互联网的组成：
- （1）边缘部分：由所有连接在互联网上的主机组成，是用户直接使用的部分。主机又称为端系统（end system）
- （2）核心部分：由大量网络和连接这些网络的路由器组成。这部分是为边缘部分提供服务的。
端系统间通信方式：客户-服务器模式 and 对等连接方式
- 客户(client)-服务器(sever)模式（C/S模式）
  - 客户是服务请求方，服务器是服务提供方
- 对等连接方式（P2P）
  - 并不区分服务请求方与服务提供方
电路交换主要特点：
- 建立连接 → 通话 → 释放资源
- 在通话的全部时间内，通话的两个用户始终占用端到端的通信资源
- 传输效率较低
分组交换主要特点：
- 采取存储转发技术
- 发送的整块数据成为报文(message)
- 发送之前，先将报文划分成一个个更小的等长数据段，加上必要控制信息组成的首部(header)或包头，构成一个分组(packet)或包。
- 主机进行信息处理，路由器用来转发分组，即进行分组交换。

1.5 计算机网络的类别

按照网络的作用范围分类：
- 广域网 WAN ：
- 域域网 MAN ：作用范围一般是一个城市。可以为一个或几个单位所有，也可以是一种公用设施，用来将多个局域网进行互连。
- 局域网 LAN ：
- 个人区域网 PAN：把属于个人的设备用无线技术连接起来
按网络使用分类：
- 公用网(public network)
- 专用网(private network)
用来把用户接入到互联网的网络：
- 接入网 AN：又称本地接入网或居民接入网。

1.6 计算机网络的性能

1.6.1 性能指标

速率：数据传送速率，也成为数据率或比特率。提到网络速率，往往指额定速率，而非运行速率。单位 bps 。
带宽：
- 信号具有的频带宽度，单位是赫兹，表示某信道允许通过的信号频带范围。
- 网络中某通道传输数据的效率，即最高数据率，单位是 bps 。
吞吐量：表示单位时间内通过某个网络的实际数据量
时延：数据从网络一端传送到另一端的时间，组成：
- 发送时延：主机或路由器发送数据帧所需时间
- 处理时延：
- 排队时延：数据帧进入路由器后需排队等待处理，等待的时间成为排队时延
- 传播时延：信道中传播的时间

$传播时延=\frac{信道长度(m)}{电磁波在信道上传播速率(m/s)}$

时延带宽积：传播时延与带宽乘积
往返时间 RTT ：数据在信道中往返一次所需时间
利用率：

$D=\frac{D_0}{1-U}$

1.7 计算机网络体系结构

1.7.1 OSI 七层协议

物理层：管理通信设备和网络媒体之间的互联互通，规范链接的电气和功能规格。
数据链路层：通过物理链接提供数据传输链路。
网络层：在两终端之间进行路径选择。
传输层：负责网络中端到端的网络通信，为虚拟电路的建立、维护、终止，传输故障检测及恢复，以及信息流的控制提供机制。
会话层：创建、管理和维护会话。同步表示层实体间的会话并管理其间的数据交换。提供高效的数据传输、服务类别以及会话、演示及应用层的异常报告功能。
演示层：保证不同系统的信息交换，涉及数据编码、格式转换、数据加密。将多种数据格式转化成通信中采用的标准表示形式。
应用层：OSI 协议最高层，离用户最近，为用户应用程序提供网络服务，不为其它层提供服务。

1.7.2 五层协议的体系结构

应用层：通过进程间的交互来完成特定网络应用，交互数据称为报文。不同网络应用需要有不同的应用层协议。
运输层：主要使用两种协议： TCP、UDP 。
网络层：把运输层产生的报文段或数据封装成包或分组进行传送。由于网络层使用 IP 协议，因此分组也叫 IP 数据报。
数据链路层：将网络层交下来的 IP 数据报组装成帧，每一帧包括数据和必要的控制信息。
物理层：上传数据单位为比特。

1.7.3 TCP/IP 四层协议

相信未来

发表于 2023-07-31 更新于 2024-01-22 分类于诗歌

作者：食指

当蜘蛛网无情地查封了我的炉台，

当灰烬的余烟叹息着贫困的悲哀，

我依然固执地铺平失望的灰烬，

用美丽的雪花写下：相信未来。

当我的紫葡萄化为深秋的露水，

当我的鲜花依偎在别人的情怀，

我依然固执地用凝霜的枯藤，

在凄凉的大地上写下：相信未来。

我要用手指那涌向天边的排浪，

我要用手掌那托起太阳的大海，

摇曳着曙光那支温暖漂亮的笔杆，

用孩子的笔体写下：相信未来。

我之所以坚定地相信未来，

是我相信未来人们的眼睛——

她有拨开历史风尘的睫毛，

她有看透岁月篇章的瞳孔。

不管人们对于我们腐烂的皮肉，

那些迷途的惆怅，失败的苦痛，

是寄予感动的热泪，深切的同情，

还是给以轻蔑的微笑，辛辣的嘲讽。

我坚信人们对于我们的脊骨，

那无数次地探索、迷途、失败和成功，

一定会给予热情、客观、公正的评定，

是的，我焦急地等待着他们的评定。

朋友，坚定地相信未来吧，

相信不屈不挠的努力，

相信战胜死亡的年轻，

相信未来，热爱生命。

Codeforces Round 877 (Div. 2)

发表于 2023-07-06 更新于 2023-12-09 分类于比赛

传送门：Codeforces Round 877 (Div. 2)

A. Blackboard List

题意：

给定包含两个数字的初始，然后进行 $n-2$ 次操作，每次操作从序列中取出两个数字（不能取同一个），将其差之绝对值加入序列，最终得到一长度为 $n$ 的序列。

现给定最终序列（乱序），求最初始数字之一。

题解：

由于新加入数字必为非负数，因此序列中的负数必定是初始数字。

若全为非负数，由于 $|a-b|\leq|a|$ 且 $|a-b|\leq |b|$ ，因此最大数字必为初始数字。

B. Minimize Permutation Subarrays

题意：

给定一 $n$ 的排列。交换两数字的位置，使得交换后序列中，能够成排列的连续子序列数目最少。

题解：

$1$ 与 $2$ 之间夹 $n$ ，这样能够使得数目恒为 $1$ ，是为最少。讨论即可

C. No Prime Differences

题意：

将 $nm$ 之内的正整数排成一个 $nm$ 矩阵，使得矩阵中任意两相邻元素差值的绝对值不为素数。

题解：

先考虑 $m\geq 5$ 时，将 $\{0, 1n, 2n, 3n, … (m-1)n\}$ 排成一列。以下是一种合适的构造方法。

设 $p=\lfloor \frac{m-1}{2}\rfloor$ 考虑两个序列

$\{0, 1*n, 2*n, ...p*n \} \\ \{(p+1)*n, (p+2)*n, ... (m-1)*n\}$

然后将两序列合成（下面序列的元素依次插入上面序列的空隙）。

若 $m=4$ ，则可构造为 $\{1n, 3n, 0, 2*n\}$

设该序列为 $A$ ，则最终矩阵可构造为 $p_{i, j}=i+A_j$

code：

void solve() {
    int n, m;
    cin >> n >> m;
    vector<int> add(m);
    int now = 0;
    for (int i = 0; i < m; i += 2) {
        add[i] = now;
        now += n;
    }
    for (int i = 1; i < m; i += 2) {
        add[i] = now;
        now += n;
    }
    if (m == 4) {
        add[0] = n;
        add[1] = 3 * n;
        add[2] = 0;
        add[3] = 2 * n;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < m; j++) cout << i + add[j] << ' ';
        cout << endl;
    }
}

D. Bracket Walk

题意：

一括号序列，从最左侧出发可以随意向左右移动（不超边界），最终停在最右侧。途经符号构成一括号序列，若该括号序列合法，则称原序列 walkable 。

现给定一括号序列 $s$ ， $q$ 次单点修改，要求求出每次单点修改后，序列是否 walkable 。

题解：

walkable 的必要条件首先是长度 $n$ 为偶数。

其次构造一序列 $A$ ，包含所有的 $i$ ，使得

$s_i=’)’$ 且 $i$ 为奇数
$s_i=’(‘$ 且 $i$ 为偶数
1. 若 $A$ 为空，则显然圆括号序列为 $()$ 重复若干次，必定 walkable。
2. 若 $A$ 非空，其中最小数字为奇数，则意味着序列开头为 $()()()…())$ ，必定非法
3. 若 $A$ 非空，其中最大数字为偶数，则意味着序列末尾为 $(()()()$ ，必定非法
4. 剩余情况， $A$ 中最小数字 $m$ 为偶数，最大数字 $M$ 为奇数，则 $m, M$ 之间符号数为偶数，其中左右括号奇偶性相同。则在 $m-1,m$ 这两个位置产生足够多的 $((….$ 来消除右侧的 $)$，然后在$M,M+1$ 两个位置产生对应数量的 $))$ 补齐即可。合法。

code：

#include<bits/stdc++.h>

using namespace std;

int main() {
    int n, q;
    set<int> s;
    string str;
    cin >> n >> q;
    cin >> str;
    auto check = [&str](int p) {
        return ((str[p - 1] == '(') ^ (p & 1));
    };
    for (int i = 1; i <= n; i++) {
        if (check(i)) s.insert(i);
    }
    /*
     * 2 9
     * */
    int pos;
    while (q--) {
        cin >> pos;
        if (n & 1) {
            cout << "NO" << endl;
            continue;
        }
        if (check(pos)) s.erase(pos);
        else s.insert(pos);
        str[pos - 1] = '(' + ')' - str[pos - 1];
        if (s.empty()) cout << "YES" << endl;
        else if ((*s.begin() & 1) || !(*s.rbegin() & 1)) cout << "NO" << endl;
        else cout << "YES" << endl;
    }
}

E. Count Supersequences

题意：

求满足以下条件的 $b$ 序列个数：

$b$ 序列含 $m$ 个正整数，所有数字均在 $[1,k]$ 内
$b$ 序列删去若干个数，顺序不变，可以得到 $a$ 序列

题解：

考虑 $dp$

$f[i][j]$ 表示含 $i$ 个正整数删去后可得到长度为 $j$ 的 $a$ 序列前缀的序列数，则有如下转移方程：

$f[i][j]= \begin{cases} f[i-1][j-1]+(k-1)*f[i-1][j],\ j<n \\ f[i-1][j-1]+k*f[i-1][j], \ j=n \end{cases}$

发现该转移方程与 $a$ 无关。

因此将 $a$ 序列设为 $n$ 个 $1$ ，然后作差法。

最终答案为：

$k^m-\sum_{i=0}^{n-1}\binom{m}{i}(k-1)^{m-i}$

code：

void solve() {
    const long long mod = 1e9 + 7;
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1, x; i <= n; i++) cin >> x;
    auto quick_pow = [&mod](int a, int b) {
        int res = 1;
        for (; b; b >>= 1) {
            if (b & 1) res = 1ll * res * a % mod;
            a = 1ll * a * a % mod;
        }
        return res;
    };
    int ans = quick_pow(k, m);
    int now = 1;
    for (int i = 0; i < n; i++) {
        ans -= 1ll * now * quick_pow(k - 1, m - i) % mod;
        ans %= mod;
        ans += mod;
        ans %= mod;
        now = 1ll * now * (m - (i+1) + 1) % mod;
        now = 1ll * now * quick_pow((i+1), mod - 2) % mod;

    }
    cout << ans << endl;
}

Educational Codeforces Round 150 (Div. 2)

发表于 2023-07-03 更新于 2024-02-27 分类于比赛

传送门：Educational Codeforces Round 150 (Rated for Div. 2)

A. Game with Board

题意：

给定初始序列为 $n$ 个 $1$ ，两人轮流行动，每次可以选择序列中若干个相同的数，剔除，并将他们的和加入序列。第一位无法行动的一方获胜。假设二人都绝对聪明，试问先手是否必胜。

题解：

分类讨论一下：

$2\leq n \leq 4$，有限轮模拟易得后手必胜。
$n\geq5$ ，则先手取 $n-2$ 个 $1$，后手只能取 $2$ 个 $1$ ，之后序列变为 $\{n-2, 2\}$ ，故先手必胜。

code：

void solve() {
    int n;
    cin >> n;
    if (n >= 5) cout << "Alice" << endl;
    else cout << "Bob" << endl;
}

C. Ranom Numbers

题意：

A, B, C, D, E 分别代表 $1, 10, 100, 1000, 10000$ 。给定一由大写字母 ABCDE 组成的串，对于某一字符，若字符串后方有严格大于它的字符，则符号为负，否则为正。字符串权值为所有字母乘上符号的权值之和。

现可以修改至多一字符，求可能的最大权值。

题解：

据说 DP 和贪心均可，这里思路是 DP 。

为了方便起见，先将字符串反转，规则也对应修正。

然后设计状态： $F[i][j][0/1]$ 代表到第 $i$ 位，目前前缀最大值为 $j$ ，且已经/未修改的最大权值。 $i$ 这一位用滚动数组滚掉，然后枚举状态的转移即可。

复杂度 $O(nMK)$ ，其中 $M=5, K=2$ 。

void solve() {
    int n;
    string s;
    cin >> s;
    n = s.length();
    reverse(s.begin(), s.end());
    int f[2][5][2];
    for (int i = 0; i < 5; i++) f[0][i][0] = f[0][i][1] = -inf;
    f[0][0][0] = 0;
    int p = 0, q = 1;
    for (auto c: s) {
        p ^= 1;
        q ^= 1;
        for (int i = 0; i < 5; i++) f[p][i][0] = f[p][i][1] = -inf;
        int x = c - 'A';
        for (int j = 0; j < 5; j++) {   //i-1位前缀最大
            for (int t = 0; t <= 1; t++) {   //
                for (int y = 0; y < 5; y++) {
                    int nt = t + (y != x);
                    int nj = max(y, j);
                    if (nt < 2) {
                        f[p][nj][nt] = max(f[p][nj][nt], f[q][j][t] + (y == nj ? digit[y] : -digit[y]));
                    }
                }
            }
        }
    }
    int ans = -inf;
    for (int i = 0; i < 5; i++) {
        ans = max(ans, f[p][i][0]);
        ans = max(ans, f[p][i][1]);
    }
    cout << ans << endl;
    return;
}

D. Pairs of Segments

题意：

给定 $n$ 条线段，用区间表示 $[l,r]$ 。若 $n$ 为偶数，且可以将 $n$ 条线段分为 $\frac{n}{2}$ 对，每一对线段相交，不成一对的线段相交，则称其 beautiful 。现问至少删去多少线段，使得剩下的线段可以 beautiful 。

题解：

$n$ 比较小。一开始以为是 $dp$ 但怎么都消除不了后效性。实际解法是——直接暴力。

首先考虑两对线段，共四条。不成对线段不相交的等价条件可以表示为：成对线段取并集，所得两条线段不相交。

因此可以直接求出 $C_n^2$ 对线段中，相交对的并集。然后找出尽量多的并线段，使其互不相交即可。互不相交可以天然保证每条线段至多用了一次。求不相交线段数目，这里用了动态开点线段树。

复杂度 $O(n^2logn)$ 。

code：

const int N = 1e6 + 5;
int lc[N << 4], rc[N << 4], dat[N << 4], cnt;
 
inline void update(int &p, int l, int r, int k, int val) {
    if (!p) p = ++cnt;
    dat[p] = max(dat[p], val);
    if (l == r) return;
    int mid = l + r >> 1;
    if (k <= mid) update(lc[p], l, mid, k, val);
    else update(rc[p], mid + 1, r, k, val);
}
 
inline int query(int p, int l, int r, int u, int v) {
    if (!p || u > v) return 0;
    if (u <= l && r <= v) return dat[p];
    int mid = l + r >> 1, ans = 0;
    if (u <= mid) ans = max(ans, query(lc[p], l, mid, u, v));
    if (v > mid) ans = max(ans, query(rc[p], mid + 1, r, u, v));
    return ans;
}
 
void solve() {
#define mp(x, y) make_pair(x, y)
#define pb(x) push_back(x)
    int n;
    cin >> n;
    vector<pair<int, int> > Line(n);
    vector<pair<int, int> > Uline;
    for (int i = 0; i < n; i++) {
        cin >> Line[i].first >> Line[i].second;
    }
    auto check = [](const pair<int, int> a, const pair<int, int> b) {
        return max(a.first, b.first) <= min(a.second, b.second);
    };
    auto uni = [](const pair<int, int> a, const pair<int, int> b) {
        return mp(min(a.first, b.first), max(a.second, b.second));
    };
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            if (!check(Line[i], Line[j])) continue;
            Uline.pb(uni(Line[i], Line[j]));
        }
    }
 
    auto cmp = [](const pair<int, int> a, const pair<int, int> b) {
        return a.second < b.second;
    };
    sort(Uline.begin(), Uline.end(), cmp);
    int ans = 0, rt = 0;
    const int inf = 1e9;
    for (auto line: Uline) {
        int rem = query(rt, -1, inf, -1, line.first - 1);
        update(rt, -1, inf, line.second, rem + 1);
        ans = max(ans, rem + 1);
    }
    cout << n - (ans << 1) << endl;
    return;
}

E. Fill the Matrix

题意：

给定一 $n*n$ 的矩阵，其中第 $i$ 列的第 $1-a_i$ 行为黑格， $a_i-n$ 行为白格，仅白格可以填数。当一个格填数 $x$ 且其正右侧格填数 $x+1$ 时，贡献一 beauty 。填入 $1-m$ 共 $m$ 个数，求最大 beauty 值。

题解：

看起来似乎比其他几道好想很多。上层所有线段都是下层线段的子集，因此从最底层线段开始枚举，填数，分裂即可。

这里还是用的线段树。注意细节。

code：

#include <bits/stdc++.h>

using namespace std;

long long ans = 0;
const int N = 2e5 + 5;
int dat[N << 2], a[N];

void build(int p, int l, int r) {
    if (l == r) return (void) (dat[p] = a[l]);
    int mid = l + r >> 1;
    build(p << 1, l, mid);
    build(p << 1 | 1, mid + 1, r);
    dat[p] = min(dat[p << 1], dat[p << 1 | 1]);
}

int ask(int p, int l, int r, int u, int v) {
    if (u <= l && r <= v) return dat[p];
    int mid = l + r >> 1, ans = N;
    if (u <= mid) ans = min(ans, ask(p << 1, l, mid, u, v));
    if (v > mid) ans = min(ans, ask(p << 1 | 1, mid + 1, r, u, v));
    return ans;
}

void solve() {
#define mp(x, y) make_pair(x, y)
#define pb(x) push_back(x)
#define pii pair<int, int>

    int n;
    cin >> n;
    vector<vector<int> > pos(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] = n - a[i];
        pos[a[i]].pb(i);
    }
    //pos[i] 值为i的位置集合(补上界n+1)
    for (int i = 0; i <= n; i++) {
        pos[i].pb(n + 1);
        sort(pos[i].begin(), pos[i].end());
    }
    long long m;
    cin >> m;

    build(1, 1, n);
    struct node {
        int l, r, pre_min;

        node(int l, int r, int pre_min) : l(l), r(r), pre_min(pre_min) {}

        bool operator<(const node X) const {
            return this->r - this->l < X.r - X.l;
        }
    };
#define Ask(l, r) ask(1, 1, n, l, r)
    priority_queue<node> q;
    q.push(node(1, n, 0));
    long long ans = 0;
    while (!q.empty()) {
        auto p = q.top();
        q.pop();
        if (p.l == p.r) continue;
        int min_num = Ask(p.l, p.r);
        if (1ll * (min_num - p.pre_min) * (p.r - p.l + 1) > m) {
            ans += (m / (p.r - p.l + 1) * (p.r - p.l)) + max(0ll, m % (p.r - p.l + 1) - 1);
            break;
        } else {
            m -= 1ll * (min_num - p.pre_min) * (p.r - p.l + 1);
            ans += 1ll * (min_num - p.pre_min) * (p.r - p.l);
            int L = std::lower_bound(pos[min_num].begin(), pos[min_num].end(), p.l) - pos[min_num].begin();
            int R = std::upper_bound(pos[min_num].begin(), pos[min_num].end(), p.r) - pos[min_num].begin();
            int pre_l = p.l;
            for (int i = L; i < R; pre_l = pos[min_num][i] + 1, i++) {
                if (pre_l < pos[min_num][i]) q.push(node(pre_l, pos[min_num][i] - 1, min_num));
            }
            if (pre_l <= p.r) q.push(node(pre_l, p.r, min_num));
        }
    }
    cout << ans << endl;
}

int main() {
    int T;
    cin >> T;
    while (T--) solve();
}

Codeforces Round 879 (Div. 2)

发表于 2023-07-01 更新于 2024-02-27 分类于比赛

传送门：Codeforces Round 879 (Div. 2)

难度适中，但菜鸡依旧。

B. Maximum Strength

题意：

$[l,r]$ 之间选两个数，使得十进制表示下各个位数的差值绝对值之和最大，位数不同则较小数补前导 $0$ 对齐。

题解：

设 $l$ 和 $r$ 位数分别为 $n$ 和 $m$ ，取的数字为 $x<y$ ，分情况讨论。

若 $n<m$ ，则最优情况为 $x$ 取 $m-1$ 个 $9$ , $y$ 保留 $r$ 的最高位，剩余位为 $0$
若 $n=m$ ，则除去相同前缀，然后 $y$ 保留最高位，剩余位为 $0$ ， $x$ 保留最高位，剩余位为 $9$ 即可。

code：

void solve() {
    string s1, s2;
    int n, m;
    cin >> s1 >> s2;
    n = s1.length();
    m = s2.length();
    if (n < m) {
        cout << (s2[0] - '0') + (m - 1) * 9 << endl;
    } else {
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (s1[i] == s2[i]) continue;
            cout << s2[i] - s1[i] + (n - i - 1) * 9 << endl;
            return;
        }
        cout << 0 << endl;
    }
    return;
}

C. Game with Reversing

题意：

给定两等长串 $S$ 和 $T$ ， Alice 和 Bob 轮流操作。Alice 每次可以替换一个字符，Bob 每次可以翻转一个串，当两串相同时，停止操作。Alice 希望操作次数尽量少， Bob 希望操作次数尽量多，求两个人都采取最优策略的情况下，实际游戏操作次数。

题解：

解释起来比较啰嗦，这里简述。

实际上 Bob 每轮操作都是相同的，因此可以假设 Bob 只翻转一个字符串 $T$ 。

对 Alice 来说，则可以有两种选择，将 $S$ 变为 $T$ 或 $rev(T)$ 。二者最小步数都容易 $O(n)$ 求出。最后根据实际的奇偶性补齐 Bob 的操作数即可。

code：

void solve() {
    int n;
    cin >> n;
    string s1, s2;
    cin >> s1 >> s2;
    int ans1 = 0, ans2 = 0;
    for (int i = 0; i < n; i++) {
        if (s1[i] != s2[i]) ++ans1;
        if (s1[i] != s2[n - i - 1]) ++ans2;
    }
    if (ans1 & 1) ans1 = ans1 * 2 - 1;
    else ans1 = ans1 * 2;
    if (ans2 & 1) ans2 = ans2 * 2;
    else if (ans2 == 0) ans2 = 2;
    else ans2 = ans2 * 2 - 1;
    cout << min(ans1, ans2) << endl;
}

D. Survey in Class

题意：

$n$ 位学生，$m$ 个知识点。第 $i$ 个学生学习了 $[l_i, r_i]$ 个知识点。

上课老师提问，每个问题至多提问一次。初始同学分数均为 $0$ ，答对加一分，答错减一分，分数可为负。求最大分差。

题解：

对于线段 $[l_1, r_1]$ 和线段 $[l_2,r_2]$ ，设 $r_1<r_2$ ，则分三种情况讨论：

$r_1<l_2$ ，则最大差值可以分别来源于两线段整段，即 $max(r_1-l_1+1, r_2-l_2+1)$ ；
$l_1\leq l_2\leq r_1 \leq r_2$，则最大差值来源于二者分别对交集取补，即 $max(r_2-r_1, l_2-l_1)$ ；
$l_2\leq l_1 \leq r_1 \leq r_2$ ，包含关系，最大差值来源于长线段对短线段取补，即 $(r_2-l_2+1)-(r_1-l_1+1)$ 。

将每条线段按右端点排序，枚举线段 $[l_2,r_2]$ ，目标是找出对应的 $[l_1, r_1]$ ，三种情况分别需要求：

右端点小于 $l_2$ 的直线中，$r-l+1$ 的最大值
相交直线中， $r$ 的最小值以及 $l$ 的最小值
左端点大于等于 $l_2$ 的直线中， $r-l+1$ 的最小值

四个值四棵动态开点线段树维护即可。

code：

#include <bits/stdc++.h>

using namespace std;
#define inf 0x7fffffff
int cnt = 0;
const int N = 4e5 + 5;
int dat[N << 5], lc[N << 5], rc[N << 5];

void update(int &p, int l, int r, int k, int val) {
    if (!p) p = ++cnt, dat[p] = inf;
    if (l == r) return (void) (dat[p] = min(dat[p], val));
    int mid = l + r >> 1;
    if (k <= mid) update(lc[p], l, mid, k, val);
    else update(rc[p], mid + 1, r, k, val);
    dat[p] = inf;
    if (lc[p]) dat[p] = min(dat[p], dat[lc[p]]);
    if (rc[p]) dat[p] = min(dat[p], dat[rc[p]]);
}

inline int query(int p, int l, int r, int u, int v) {
    if (!p) return inf;
    if (u <= l && r <= v) return dat[p];
    int mid = l + r >> 1, res = inf;
    if (u <= mid) res = min(res, query(lc[p], l, mid, u, v));
    if (v > mid) res = min(res, query(rc[p], mid + 1, r, u, v));
    return res;
}

bool cmp(pair<int, int> A, pair<int, int> B) {
    return A.second == B.second ? A.first < B.first : A.second < B.second;
}

void solve() {
#define mp(x, y) make_pair(x, y)
    int t1 = 0, t2 = 0, t3 = 0, t4 = 0;
    int n, m;
    cin >> n >> m;
    vector<pair<int, int> > Stu(n);
    for (int i = 0, l, r; i < n; i++) {
        cin >> l >> r;
        Stu[i] = mp(l, r);
    }
    sort(Stu.begin(), Stu.end(), cmp);
    int ans = 0;
    for (auto stu: Stu) {
        int l = stu.first, r = stu.second;
        int rem;
        rem = -query(t1, 0, m, 0, l - 1);
        if (rem != -inf) ans = max(ans, max(rem << 1, (r - l + 1) << 1));
        update(t1, 0, m, r, l - r - 1);

        rem = query(t2, 0, m, l, r);
        if (rem != inf) ans = max(ans, (r - rem) << 1);
        update(t2, 0, m, r, r);

        rem = query(t3, 0, m, l, r);
        if (rem != inf) ans = max(ans, (l - rem) << 1);
        update(t3, 0, m, r, l);

        rem = query(t4, 0, m, l, r);
        if (rem != inf) ans = max(ans, ((r - l + 1) - rem) << 1);
        update(t4, 0, m, l, r - l + 1);
    }
    cout << ans << endl;
    return;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

E. MEX of LCM

题意：

题如其名。给定 $n$ 个数，则对应的有 $C_n^2$ 个连续子序列。求所有子序列数值 $lcm$ 的 $Mex$ 。

题解：

同样是利用好值域。对于区间 $[l,r]$ ，固定住右端点 $r$ ，则至多还剩下 $r$ 个左端点，对应 $r$ 个区间。这 $r$ 个区间有多少 $lcm$ 值？从 $l=r$ 开始，每次向左添加一个数， $lcm$ 要么不变，要么至少翻一倍，因此 $lcm$ 值的数目是 $log$ 级别的。因此整个序列所有 $lcm$ 值的数目不超过 $nlogn$ ，迭代求出然后求 $Mex$ 即可。复杂度 $O(nlogn)$

code：

inline long long lcm(long long x, long long y) {
    return x / __gcd(x, y) * y;
}

void solve() {
    int n;
    cin >> n;
    long long inf = 1ll * n * n + 2;
    vector<int> num(n);
    for (int i = 0; i < n; i++) cin >> num[i];
    set<long long> s;	//以r-1为右端点的lcm序列
    set<long long> rem; //以r为右端点的lcm序列
    set<long long> ans;	//所有lcm序列
    for (auto x: num) {
        for (auto y: s) {
            long long p = lcm(y, x);
            if (p <= inf) rem.insert(p);
        }
        rem.insert(x);
        s.clear();
        for (auto y: rem) s.insert(y);
        rem.clear();

        for (auto y: s) ans.insert(y);
    }
    long long now = 1;
    ans.insert(inf);
    for (auto x: ans) {
        if (x != now) {
            cout << now << endl;
            return;
        }
        ++now;
    }
}

数理思维

发表于 2023-07-01 更新于 2023-12-09 分类于杂项

一、“决不能把任何我没有明确地认识其为真的东西当作真的加以接受，也就是说，小心避免仓促的判断和偏见，只把那些十分清楚明白地呈现在我的心智之前，使我根本无法怀疑的东西放进我的判断之中”。

在数理逻辑论证推理中，务必做到毫无破绽。防范”千里之堤，溃于蚁穴“的局面。更直观地来说，论证必须有从底层起始的依据。

在日常生活中，这一条也同样适用。我们处在一个信息爆炸的时代，很多时候困扰我们的并不是信息资源的匮乏，而是信息茧房的拘束以及信息泛滥的迷茫。保持理性，对信息加以筛选，过滤掉无依据的信息。

二、“把我所考察的每一个难题，都尽可能地分成细小的部分，直到可以而且适于加以圆满解决的程度为止”。

比较典型的分而治之思想。当整体带有规律性时，局部往往也具有与整体相同或相似的规律性，通过不断地划分，最终将问题转化为一个个显然或已解决的子问题。从个别、特殊到一般的方法。

三、“按照次序引导我的思想，以便以最简单最容易认识的对象开始，一点一点上升到对复杂的对象的认识，即便是那些彼此间没有自然的先后次序的对象，我也要给它们设定一个次序”。

从易到难，从简单到复杂地进行分析、解决，而不至于迷乱。

四、“把一切情形尽量完全地列举出来，尽量普遍地加以审视，使我确信毫无遗漏。”

如其所言，思维缜密，考虑周全，确保推理覆盖到所有情况。

摘自：笛卡尔《方法论》

人生没有目的，只有过程，所谓的终极目的是虚无的。——人的情况和树相同。它愈想开向高处和明亮处，它的根愈要向下，向泥土，向黑暗处，向深处，向恶——千万不要忘记。我们飞翔得越高，我们在那些不能飞翔的人眼中的形象越是渺小。

ChatGPT 指北

发表于 2023-06-30 更新于 2024-06-10 分类于杂项

Here's something encrypted, password is required to continue reading.

阅读全文 »

Codeforces Round 880(Div. 2)

发表于 2023-06-29 更新于 2023-12-09 分类于比赛

挂个传送门：Dashboard - Codeforces Round 880 (Div. 2) - Codeforces

评价是，切完ABC蹲大牢

B. Astrophysicists

题意：

$k*g$ 银币分配给 $n$ 人，设一个人分到 $x$ 银币，$r=x \mod g$ 对每人有补正如下：

若 $r\geq \lceil \frac{g}{2} \rceil$，则向上修正至 $x+(g-r)$；
否则，向下修正至 $x-r$ .

求分配完后，剩下的银币数目之和最小值。

题解：

什么黑心资本家出的题。

考虑一个人分配到的银币，从 $0$ 增加至 $g$ 。增加至 $\lceil \frac{g}{2}\rceil$ 前，经补正他所获得银币为 $0$ ，原先分配银币即剩下；增加至 $\lceil \frac{g}{2}\rceil$ 后，我们需要额外的银币为其补正。故对一个人来说，我们的收益和他分配的银币呈一个由两直线构成的分段函数，从 $0$ 开始并且回到 $0$ 。我们的最大收益点在 $p=\lceil \frac{g}{2}\rceil-1$ 。

此时可以分成两种情况讨论：

若 $np \geq kg $ ，那所有人贪心分配（至多 $p$ ），最后每个人分配到 $0$ ，方案显然最优，结果为 $ k*g $ 。
若$np< kg$，最优分配结果为$g\lfloor \frac{p*n}{g} \rfloor$ 。

讨论下第二种情况，为什么是这个式子。

易知，最优方案不存在向上修正。设第 $i$ 个人分配到 $x_i$ 银币，则有$\sum x_i = k*g$，因此我们的收益 $income$ 满足 $income=\sum (x_i\% g)\equiv (\sum x_i)\% g\equiv 0 $ 。这是一个比较重要的性质，答案必定是 $g$ 的倍数。

设 $income=kg$ ，则必有 $kg \leq pn $ （答案上限就是 $pn$ ），故 $income = kg = g \lfloor \frac { p*n } { g } \rfloor $

code：

void solve() {
    long long n, k, g;
    cin >> n >> k >> g;
    long long p = ((g + 1) >> 1) - 1;
    if (p * n >= k * g) {
        cout << k * g << endl;
    } else {
        cout << p * n / g * g << endl;
    }

}

C. K-th equality

题意：

构造第 $k$ 大字典序字符串，其中字符串形如 $A$ 位数 $+B$ 位数 $=C$ 位数。

题解：

体感很简单的一道题。

设 $x$ 位数的范围为 $[L_x, R_x)$

由于 $A\leq 6$，因此枚举 $x+y=z$ 中的 $x$ 。

接下来寻找对 $y$ 的限制条件。

$L_B\leq y<R_B$
$L_C\leq z< R_C$ ，即 $L_C\leq x+y <R_C$

由此可得限制条件 $max\{L_B,L_C-x\}\leq y<min\{R_B,R_C+x\}$

然后边统计边算即可。复杂度 $O (10^A)$

code：

const int mn[8] = {0, 1, 10, 100, 1000, 10000, 100000, 1000000};

void solve() {
    int A, B, C;
    long long k;
    cin >> A >> B >> C >> k;
    for (int mx = mn[A + 1], i = mn[A]; i < mx; i++) {
        int l = max(mn[C] - i, mn[B]);
        int r = min(mn[C + 1] - i, mn[B + 1]);
        if (l >= r) continue;
        if (k <= r - l) {
            cout << i << " + " << l + k - 1 << " = " << i + l + k - 1 << endl;
            return;
        } else k -= r - l;
    }
    cout << -1 << endl;
    return;
}

E. Twin Clusters

题意：

给定长为 $2^{k+1}$ 的一序列，值域为 $[0,4^k)$ 。求原序列两不相交子区间，使得两子区间中数字的异或和相同。

题解：

瞄了眼 Tutorial ，不太好想。一开始想过类似于分块的思路，实际解法也差不多，不过只取一个块。

先关注二进制下低 $k$ 位。算上空串，共有 $2^{k+1}+1$ 个值，但实际上低 $k$ 位值域 $[0,2^k-1]$ 共 $2^k$ 个值，因此根据鸽巢原理，我们可以匹配出 $2^k+1$ 个区间 $(l_i, r_i]$，使得这每个区间 $S_{r_i} \ xor\ S_{l_i}$ 的低$k$ 位均为 $0$ 。

接下来关注这些线段的高 $k$ 位。采取同样的方法，根据鸽巢原理，必定存在两个子区间高 $k$ 位的异或和相同，取这两子区间的交即为结果。

code：

void solve() {
#define mp(x, y) make_pair(x, y)
    int k, n;
    cin >> k;
    n = (1 << (k + 1));
    vector<long long> g(n + 1), s(n + 1);
    vector<pair<long long, long long> > Line;
    unordered_map<long long, long long> mp;
    mp[0] = 0;
    g[0] = s[0] = 0;
    long long lbit = (1ll << k) - 1;
    long long hbit = (((1ll << (k << 1)) - 1) ^ lbit);
    for (int i = 1; i <= n; i++) {
        cin >> g[i];
        s[i] = s[i - 1] ^ g[i];
        long long p = (s[i] & lbit);
        if (mp[p] || p == 0) Line.push_back(mp(mp[p], i));
        mp[p] = i;
    }
    unordered_map<long long, int> pos;
    int i = 0;
    for (auto line: Line) {
        ++i;
        long long p = ((s[line.second] ^ s[line.first]) & hbit);
        if (pos[p] != 0) {
            auto l1 = Line[pos[p] - 1], l2 = line;
            if (l1.second <= l2.first) {
                cout << l1.first + 1 << ' ' << l1.second << ' ' << l2.first + 1 << ' ' << l2.second << endl;
            } else {
                cout << min(l1.first, l2.first) + 1 << ' ' << max(l1.first, l2.first) << ' ' << l1.second + 1 << ' '
                     << l2.second << endl;
            }
            return;
        } else pos[p] = i;
    }

}

D. Lottery

题意：

给定 $n$ 个人，每人买一张彩票，票号在 $[0,m]$ 范围内。设开奖号为 $x$ ，则票号距离 $x$ 最近的 $k$ 人中奖，平局情况则编号小的获胜。作为第 $n+1$ 人，你编号最大，求最小位置，使得能够使你中奖的编号尽可能多。

题解：

非常繁琐的一道题。先来看这幅图（截自 tutorials ）：

假设当前选择编号为 $c$ ，$c$ 的前 $k$ 名为 $a$ ，后 $k$ 名为 $b$ 。则中奖区间为 $(\lfloor \frac{a+c}{2} \rfloor, \lceil \frac{b+c}{2} \rceil)$ 。由此计算结果。

接下来讨论需要枚举哪些 $c$ 。由上面图可知，处在 $(d,e)$ 区间内时，中奖区间虽然改变，但实际中奖区间长度不变（$a$ 和 $b$ 没有变化）。故我们只需讨论 $n$ 个人所选号码的前后两三个数即可。当然，特别考虑边界情况。

输入量较大，需要注意 $IO$ 效率。

code：

#include<bits/stdc++.h>

using namespace std;

vector<long long> v;
int nowl, nowr;
int n, k;
long long m;

long long calc(long long now_pos) {
    while (nowl < n && v[nowl] < now_pos) ++nowl;
    while (nowr < n && v[nowr] <= now_pos) ++nowr;
    long long posl = nowr - k < 0 ? 0 : (now_pos + v[nowr - k]) / 2 + 1;
    long long posr = nowl + k - 1 >= n ? m : (now_pos + v[nowl + k - 1] - 1) / 2;
    return max(0ll, posr - posl + 1);
}

void solve() {
    v.clear();
    cin >> n >> m >> k;
    long long c;
    for (int i = 0; i < n; i++) {
        cin >> c;
        v.push_back(c);
    }
    v.push_back(m + 1);
    sort(v.begin(), v.end());
    nowl = nowr = 0;
    long long res_pos = 0, ans = calc(0);
    for (int i = 0; i < n; i++) {
        long long bl = i == 0 ? max(0ll, v[i] - 2) : max(v[i] - 2, v[i - 1] + 3);
        long long br = min(v[i] + 2, m);
        for (long long now_pos = bl; now_pos <= br; now_pos++) {
            long long p = calc(now_pos);
            if (p > ans) {
                ans = p;
                res_pos = now_pos;
            }
        }
    }
    cout << ans << ' ' << res_pos << endl;
    return;
}

int main() {
    std::ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    solve();
}

F. Doctor’s Brown Hypothesis

题意：

给定一有向图，求无序点对 $(u, v)$ 的数目，使得 $u$ 和 $v$ 相互之间存在着长度为 $k$ 的路径，其中 $u=v$ 也被允许。

题解：

不会。稍微翻译下 tutorial 。

突破口在 $k\geq n^3$ 。显然对于所有满足答案的点对，两点都在同一个强连通分量内。于是讨论范围缩减到同一个 $SCC$ 。对强连通分量内的所有环的大小，存在一个最大公约数 $g$ 。将所有的边 $$ 按照 $t=(s+1)mod\ g$ 进行染色。由于 $k$ 比较大，所以可以认为颜色相同的点都是等价的。

对于一个连通分量内，满足条件的点对有以下两种：

$g|k$ ，则所有颜色相同点对满足条件。
$2|g$ 且 $k\equiv g/2\ mod \ g$ ，则所有颜色差值为 $g/2$ 的点对满足条件

code：

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
int n, m;
long long k;
vector<int> v[N];
vector<int> vec[N];
int col[N], cnt_col;
int _stack[N], _t, dfn[N], low[N], cnt, siz[N];
bool book[N];

inline void tarjan(int x) {
    //强连通分量
    dfn[x] = low[x] = ++cnt;
    _stack[++_t] = x;
    book[x] = true;
    for (auto ver: v[x]) {
        if (!dfn[ver]) {
            tarjan(ver);
            low[x] = min(low[x], low[ver]);
        } else if (book[ver]) low[x] = min(low[x], dfn[ver]);
    }
    if (dfn[x] == low[x]) {
        ++cnt_col;
        int p;
        do {
            p = _stack[_t];
            col[p] = cnt_col;
            ++siz[cnt_col];
            book[p] = false;
            --_t;
        } while (p != x);
    }
}

int flag[N], dis[N];
bool solved[N];

inline void dfs(int x, int d, int des) {
    dis[x] = d;
    flag[x] = des;
    for (auto ver: vec[x]) {
        if (flag[ver] != des) dfs(ver, d + 1, des);
    }
}

int num[N];

int tag[N];

inline bool draw_col(int x, int now, int base_num, int des) {
    //尝试染色
    num[x] = now;
    tag[x] = des;
    bool Flag = true;
    for (auto ver: vec[x]) {
        if (!Flag) return false;
        if (tag[ver] != des) Flag &= draw_col(ver, (now + 1) % base_num, base_num, des);
        else Flag &= (num[ver] == ((num[x] + 1) % base_num));
    }
    return Flag;
}

int cnt_num[N];

inline void Draw_col(int x, int now, int base_num, int des) {
    //染色，统计数目
    num[x] = now;
    tag[x] = des;
    ++cnt_num[now];
    for (auto ver: vec[x]) {
        if (tag[ver] != des) Draw_col(ver, (now + 1) % base_num, base_num, des);
    }
}


int main() {
    cin >> n >> m >> k;
    for (int i = 1, x, y; i <= m; i++) {
        cin >> x >> y;
        v[x].push_back(y);
    }
    for (int i = 1; i <= n; i++) {
        if (!col[i]) tarjan(i);
    }
    for (int i = 1; i <= n; i++) {
        for (auto y: v[i]) {
            if (col[i] == col[y]) vec[i].push_back(y);
        }
    }
    int search_num = 0;
    long long ans = 0;
    for (int i = 1; i <= n; i++) {
        if (solved[col[i]]) continue;
        solved[col[i]] = true;
        if (siz[col[i]] == 1) continue;
        int x = i, y = vec[x][0];
        int d = 0;
        dfs(y, 0, y);
        d += dis[x] + 1;
        int g = 1;
        for (int j = 2; j * j <= d; j++) {
            if (d % j != 0) continue;
            int p = j, rem_num = 1;
            bool now_flag = true;
            while (d % p == 0) {
                ++search_num;
                if (now_flag && draw_col(x, 0, p, search_num)) rem_num = p;
                else now_flag = false;
                p *= j;
            }
            d /= (p / j);
            g *= rem_num;
        }
        if (d > 1 && (++search_num) && draw_col(x, 0, d, search_num)) g *= d;
        for (int j = 0; j < g; j++) cnt_num[j] = 0;
        ++search_num;
        Draw_col(x, 0, g, search_num);
        if (k % g == 0) {
            for (int j = 0; j < g; j++) ans += 1ll * cnt_num[j] * (cnt_num[j]+1) / 2;
        } else if (g % 2 == 0 && k % g == g / 2) {
            for (int j = 0; j < g / 2; j++) ans += 1ll * cnt_num[j] * cnt_num[j + g / 2];
        }
    }
    cout << ans << endl;
}

2.1 物理层的基本概念

2.2 数据通信的基础知识

2.2.1 数据通信系统的模型

2.2.2 有关信道(channel)的几个基本概念

2.2.3 信道极限容量

2.3 物理层下面的传输媒体

2.3.1 导引型传输媒体

1. 双绞线

2. 同轴电缆

3. 光缆

4. 架空明线

2.3.2 非导引型传输媒体

2.3.2.1 微波通信

2.3.2.2 卫星通信

2.4 信道复用技术

2.4.1 频分复用、时分复用与统计时分复用

2.4.2 波分复用

2.4.3 码分复用

2.5 数字传输系统

2.6 宽带接入技术

2.6.1 ADSL 技术

2.6.2 光纤同轴混合网

2.6.3 FTTx 技术

1.1 概念

1.2 计算机简史

1.2.1 第一代：真空管

1.2.2 第二代：晶体管

1.2.3 第三代：中小规模集成电路

1.2.4 第四代：（超）大规模集成电路

1.3 计算机发展

1.3.1 摩尔定律

1.4 计算机性能

1.4.1 CPU 性能

1.4.2 性能设计的基本原则

第1章 概述

1.1 计算机网络在信息时代的作用

1.2 互联网概述

1.3 互联网的组成

1.5 计算机网络的类别

1.6 计算机网络的性能

1.6.1 性能指标

1.7 计算机网络体系结构

1.7.1 OSI 七层协议

1.7.2 五层协议的体系结构

1.7.3 TCP/IP 四层协议

A. Blackboard List

B. Minimize Permutation Subarrays

C. No Prime Differences

D. Bracket Walk

E. Count Supersequences

A. Game with Board

C. Ranom Numbers

D. Pairs of Segments

E. Fill the Matrix

B. Maximum Strength

C. Game with Reversing

D. Survey in Class

E. MEX of LCM

一、“决不能把任何我没有明确地认识其为真的东西当作真的加以接受，也就是说，小心避免仓促的判断和偏见，只把那些十分清楚明白地呈现在我的心智之前，使我根本无法怀疑的东西放进我的判断之中”。

二、“把我所考察的每一个难题，都尽可能地分成细小的部分，直到可以而且适于加以圆满解决的程度为止”。

三、“按照次序引导我的思想，以便以最简单最容易认识的对象开始，一点一点上升到对复杂的对象的认识，即便是那些彼此间没有自然的先后次序的对象，我也要给它们设定一个次序”。

四、“把一切情形尽量完全地列举出来，尽量普遍地加以审视，使我确信毫无遗漏。”

B. Astrophysicists

C. K-th equality

E. Twin Clusters

D. Lottery

F. Doctor’s Brown Hypothesis

第1章概述